3 Types de mouvements - trajectoires associées
Définition : Trajectoire
Définition : Mouvement de rotation
Un solide 2 est en rotation par rapport à un solide 1 si et seulement si, il existe à chaque instant une droite du solide 2 immobile par rapport au solide 1.
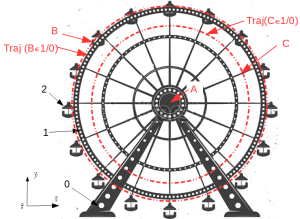
Les trajectoires de tous les points sont des cercles concentriques. Il faut donc définir le centre et le rayon.
Exemple :
Mvt 1/0 : rotation d'axe \((A,\vec{z})\)
Traj (B ∈1 /0) : cercle de centre A et de rayon [AB]
Traj (C ∈1 /0) : cercle de centre A et de rayon [AC]
Définition : Mouvement de translation
Mouvement de translation : deux segments sécants du solide restent parallèles à eux-même pendant le mouvement. Les trajectoires de tous les ponts du solide sont parallèles.
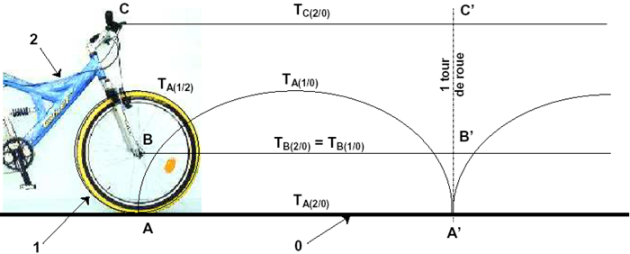
Exemple : Bicyclette
Soit A le point de contact entre la roue 1 et le sol 0.
Soit B le centre de l'articulation entre la roue 1 et le cadre 2.
Soit C un point appartenant au cadre 2.
On peut noter la nature des trajectoires suivantes :
\(T_{C \in 2/0}\). : droite horizontale (rectiligne horizontale)
\(T_{B \in 1/2}\) : point coïncident (fixe)
\(T_{B \in 1/0}\) : droite horizontale
\(T_{B \in 2/0}\) : droite horizontale
\(T_{A \in 2/0}\) : droite horizontale
\(T_{A \in 1/2}\) : cercle de centre B et de rayon BA
\(T_{A \in 1/0}\) : cycloïde