3 Degrés de liberté et liaisons
Notion de degré de liberté
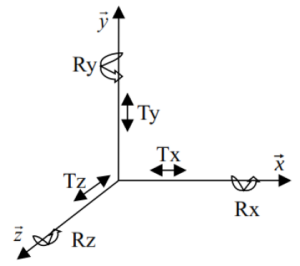
Lorsque deux pièces se touchent elles forment une liaison. Les surfaces de contact empêchent certains degré de liberté d'exister. A une liaison, on peut associer un tableau complété avec :
_ 1 si le degré de liberté est autorisé
_ 0 si le degré de liberté est empêché
Mouvement suivant l'axe | T (mouvement de translation) | R (mouvement de rotation) |
|---|---|---|
\(\vec{x}\) | ||
\(\vec{y}\) | ||
\(\vec{z}\) |
Une autre représentation possible de ce tableau et de remplacer le 1 par la lettre du mouvement avec en indice l'axe exemple Tx , Rz ...
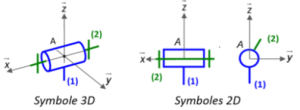
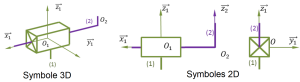
Exemple : Modélisation d'un mouvement élémentaire par une liaison pivot ou glissière
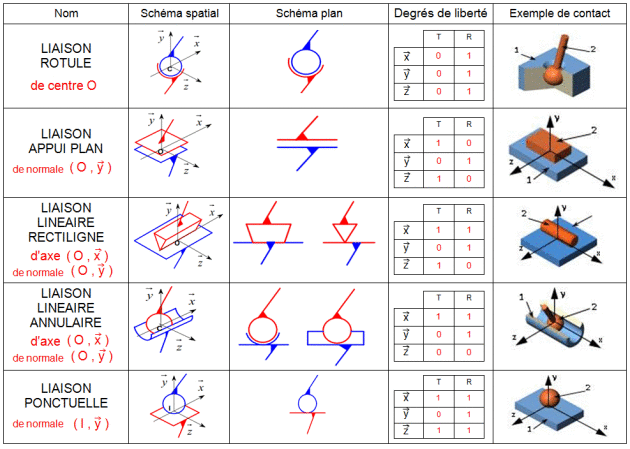
Méthode : Liaisons normalisées
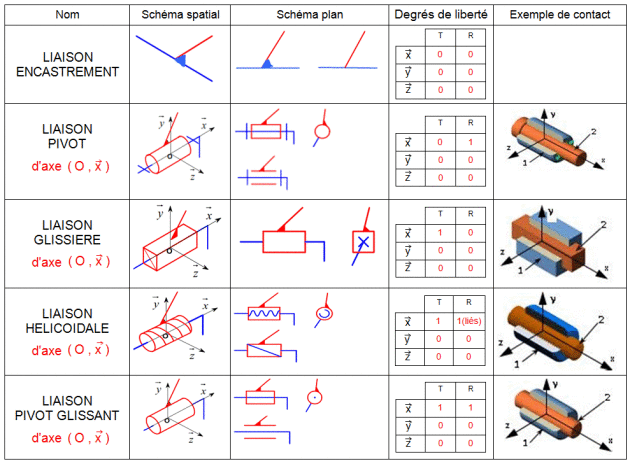
Il existe 11 liaisons élémentaires, représentées par des symboles normalisés :
Pour étudier une liaison entre deux solides, on utilise la démarche suivante :
Identifier le contact,
Définir les D.D.L. possibles,
Définir la liaison.
Pendant l'étude de la liaison, on ne modifie pas les contacts fonctionnels et on étudie que les 2 pièces ou ensembles isolés du reste du mécanisme.