Equations de droite
Equation d'une droite
Dans un repère du plan \((O, \, \vec{x}, \vec{y})\), lorsqu'une droite n'est pas parallèle à l'axe des ordonnées, elle est la représentation graphique d'une fonction affine.
Elle admet une équation de la forme : \(\boxed{ \large{ y = ax +b }}\) avec \(a, b \in \mathbb{R}\)
\(a\) est le coefficient directeur de la droite.
Il se détermine graphiquement par le quotient :
\(\boxed{ \large{ a = \frac{y_B - y_A} {x_B - x_A} }}\)
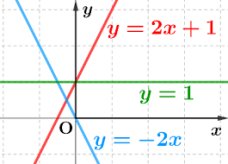
\(b\) est l'ordonnée à l'origine de la droite.
Lorsque \(b\) \(= 0\), la droite passe par l'origine du repère et est la représentation graphique d'une fonction linéaire. Sa détermination est possible par deux moyens :
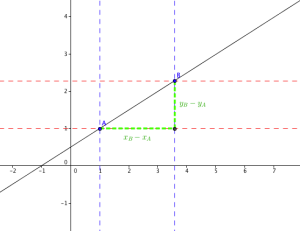
Graphiquement : on identifie la valeur de \(b\) sur l'axe des ordonnées.
Analytiquement : on utilise l'équation de la droite et les coordonnées d'un des points de la droite (Si \(A \in\) droite (\(d\)) alors \(b = y_A - ax_A\)).
Modélisation par des fonctions linéaires
Lors des pratiques expérimentales ou de simulation, il est fréquent d'effectuer des mesures. Celles-ci sont relevées et stockées en général dans un tableau de valeurs. Ces mesures permettent d'établir graphiquement un nuage de points qui peut être proche notamment d'un modèle mathématique de fonction linéaire.
Remarque :
Il existe d'autres modèles mathématiques traduisant des nuages de points plus particuliers :
fonction sinusoïdale : \(y = \sin(x) \, ; y=\cos(x) \, ...\)
fonction logarithme : \(y = ln(x) \, ;y=log_10(x)\)
fonction exponentielle : \(y=e^x\)
fonction puissance : \(y = x^b\)
...
Méthode : Traitement de résultats à partir d'un nuage de points
Relever les valeurs des grandeurs physiques obtenues par expérimentation ou simulation :
Tableau des mesures U (en V)
4,39
4,37
4,34
4,30
4,28
4,26
4,25
4,20
I (en mA)
22
34
41
50
62
69
80
94
Placer les points dans un graphique (ex : \(U=f(I)\)).
Tracer la droite-modèle la plus proche des points expérimentaux (en minimisant les écarts).
Déterminer l'équation de la droite-modèle sous la forme \(y=ax+b\).
